Im Jahr 1814 drückte der Mathematiker Pierre-Simon Laplace einen futuristischen Gedanken aus: Wenn eine Intelligenz zu einem bestimmten Zeitpunkt alle im Universum herrschenden Naturgesetze kennt sowie die Lage und Geschwindigkeit aller Teilchen, aus denen es aufgebaut ist, dann könnte man den Zustand des Universums zu jedem zukünftigen und vergangenen Zeitpunkt präzise berechnen. Darin drückt sich ein sehr deterministisches Weltbild aus: Wie in einem Uhrwerk laufen alle Prozesse der Welt präzise und streng berechenbar ab. Die moderne Wissenschaft hat gewichtige Argumente gegen diesen sogenannten Laplaceschen Dämon ins Feld geführt. Zum einen hat die Quantenphysik gezeigt, dass es unmöglich ist, Ort und Impuls atomarer Teilchen gleichzeitig präzise zu bestimmen.

Ein anderes Gegenargument kommt aus der Chaostheorie, einer modernen mathematischen Disziplin. Darin werden dynamische Prozesse untersucht, also Prozesse, bei denen sich laufend etwas ändert. Die Entwicklung des Wetters, die Lage der Kugeln bei einer laufenden Lottoziehung, die Bewegung von Himmelskörpern oder die Wirtschaftsentwicklung sind Beispiele solcher dynamischer Systeme. Es konnte gezeigt werden, dass viele dynamische Systeme grundsätzlich nicht vorhersehbar sind, obwohl sie teils durch ganz einfache Gesetze gesteuert werden. Das liegt einerseits daran, dass es unmöglich ist, die Zustände sämtlicher beteiligter Teilchen zu Beginn des Prozesses präzise zu messen, und andererseits daran, dass winzige (und eben unvermeidliche) Fehler beim Messen der Startbedingungen zu völlig unterschiedlichen Langzeitentwicklungen führen. Dieses in der Chaostheorie Sensitivität genannte Phänomen wird populärwissenschaftlich oftmals als Schmetterlingseffekt bezeichnet: Schon kleine Änderungen der Anfangsbedingungen wie etwa der Flügelschlag eines Schmetterlings kann der Wetterentwicklung eine ganz andere Richtung geben.

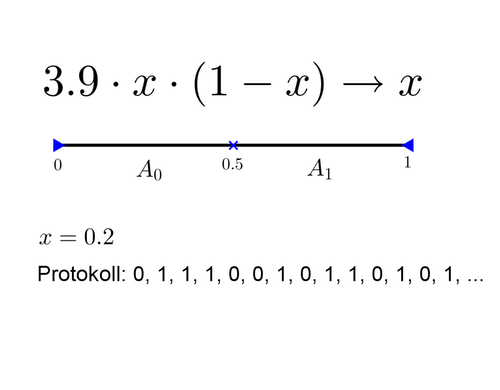
Betrachten wir nun ein eindrückliches Modell: Die Abbildung zeigt eine Formel, in die wir irgendeine Zahl x zwischen 0 und 1 einsetzen sollen, zum Beispiel 0.2. Nun berechnen wir das Resultat des Ausdrucks 3.9x(1-x) und nennen dieses Resultat wieder x. So fahren wir lange Zeit fort: Jede neu erhaltene Zahl stecken wir in denselben Ausdruck und erhalten dadurch eine weitere Zahl. Von all diesen so entstandenen Zahlen betrachten wir nur jede dritte. Von jeder dritten Zahl entscheiden wir, ob sie zwischen 0 und 0.5 oder ob sie zwischen 0.5 und 1 liegt. Im ersten Fall notieren wir eine 0, im zweiten eine 1. So entsteht das Protokoll in der Abbildung.

In der Chaostheorie kann man nun beweisen, dass jedes nur denkbare Protokoll tatsächlich vorkommt, dass sich also für jede beliebige 0-1-Folge ein x finden lässt, welches exakt diesem Protokoll folgt. Das bedeutet, dass wir nichts über die Zukunft eines solches Prozesses sagen können, wenn wir ein Anfangsstück eines Protokolls kennen, weil ja jede nur denkbare Fortsetzung auch tatsächlich vorkommt. Messen wir also den Zustand des Prozesses eine gewisse Zeit lang, so bleibt uns seine Zukunft dennoch verborgen. Das meint man, wenn man in der Mathematik von Chaos spricht.

Übrigens: Wie lauten die ersten 20 Einträge des Protokolls von x = 0.21?

Armin P. Barth ist Gymnasiallehrer an der Kantonsschule Baden und Autor. Die Lösung erscheint am nächsten Dienstag auf der Seite Leben&Wissen.