Eines der aufsehenerregendsten Ergebnisse der modernen Mathematik ist ohne Zweifel der Satz von Banach-Tarski. Mit ihrem Beweis im Jahr 1924 ist Stefan Banach und Alfred Tarski etwas überaus Verblüffendes geglückt. Sie haben nämlich bewiesen, dass es möglich ist, eine Kugel in Teile zu zerlegen, die dann – anders zusammengesetzt – zwei identische Kugeln von je dem gleichem Volumen wie die ursprüngliche Kugel ergeben. Dazu genügt es, die Teile, in die die erste Kugel zerlegt wird, geschickt zu verschieben und zu drehen.

Das erscheint auf den ersten Blick völlig unglaubwürdig, weil uns bei der Rezeption dieses Sachverhaltes eine Idee im Wege steht, die Idee nämlich, dass alle Teile, in die eine Kugel möglicherweise zerlegt werden kann, zwingend ein Volumen haben müssen. Wie sollen dann bitteschön die Teile, die zusammen das Volumen einer Kugel ergeben, allein durch ein paar Bewegungen zwei neue Kugeln mit je demselben Volumen wie die erste Kugel ergeben? Aus eins mach zwei geht doch nicht.

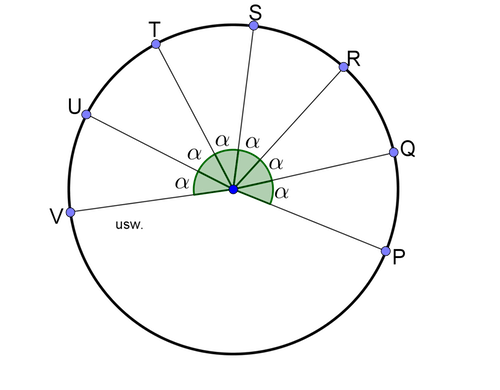
Der Beweis ist leider zu lang und zu kompliziert für diese Kolumne; insbesondere benötigt man dafür einiges an Mengenlehre und Gruppentheorie. Aber wir können trotzdem eine zentrale Idee aufzeigen. Stellen Sie sich vor, dass wir irgendwo auf einer Kreislinie einen Punkt P auswählen (Abbildung). Von dort aus tragen wir immer unter demselben Winkel α neue Punkte Q, R, S, … ab. Bald werden wir zum ersten Mal eine volle Umdrehung überschreiten, aber wir werden nicht auf P treffen, wenn wir den Winkel geschickt wählen. Wir fahren unendlich lange so fort. Auf diese Weise erhalten wir unendlich viele Punkte auf der Kreislinie, die wir uns durchnummeriert denken können. Und es werden unendlich viele Punkte auf der Kreislinie übrig bleiben.

Nun verordnen wir unseren Punkten eine Drehung. Gleichzeitig soll jeder Punkt um den Winkel α weiterdrehen. Dadurch gelangt P zu Q, Q zu R, R zu S, und so weiter, aber kein Punkt zu P. Der Punkt P wird sozusagen frei. Damit haben wir in der Tat eine paradoxe Situation geschaffen: Allein durch Drehung eines Teils des Kreises kommt ein Punkt abhanden. Oder, wenn wir zurückdrehen: Allein durch Drehung eines Teils des Kreises zaubern wir einen neuen Punkt aus dem Nichts herbei.

So ähnlich kann man die Kugel so in Teile zerlegen, dass durch einfache Bewegungen der Teile so viele neue Punkte entstehen, dass daraus eine zusätzliche neue Kugel erschaffen werden kann. Unser obiges Beispiel lässt aber schon ahnen, dass die Teile nicht durch Zerschneiden der Kugel mit einem Messer erhalten werden kann; die Teile sind überaus komplizierte Punktmengen, die man niemals physikalisch bilden und denen man nicht einmal ein Volumen zuordnen kann. Banach und Tarski lehren uns, sehr vorsichtig mit dem Begriff des Volumens umzugehen. Nicht alle Teilmengen irgendeines realen Gegenstandes besitzen automatisch ein Volumen. Denn sonst könnte man Dinge aus dem Nichts entstehen lassen.

Übrigens: Welche Eigenschaft muss ein Winkel haben, damit auf diese Weise niemals ein Punkt auf einen schon existierenden Punkt fällt?

Armin P. Barth ist Gymnasiallehrer an der Kantonsschule Baden und Autor. Die Lösung erscheint am nächsten Dienstag auf der Seite Leben&Wissen.