Als Student habe ich häufig und gerne Billard gespielt – und erst später erfahren, dass dieses Spiel auch aus mathematischer Sicht hochinteressant ist. Erste Erwähnungen von Spielen, bei denen man Bälle mit Stöcken anstösst, gehen bis ins 13. Jahrhundert zurück, und vom französischen König Ludwig XI weiss man, dass er im Jahr 1470 einen Billardtisch erworben hatte. Aber inwiefern bietet Billard auch mathematischen Genuss?

Zunächst: Mathematisches Billard unterscheidet sich vom realen Spiel und ist aus anderen Gründen spannend. Beim mathematischen Billard ist der Tisch perfekt eben und die Kugel punktförmig, womit insbesondere der «Effet» wegfällt, mit dem geübte Spieler die Kugel auf leicht gekrümmte Bahnen schicken. Auch Reibung gibt es nicht, so dass die Kugel also nie abbremst und theoretisch nie zum Stillstand kommt. Interessant ist aber die folgende mathematische Frage: Wenn man eine einzige Kugel irgendwo auf dem Tisch platziert und in irgendeine Richtung anstösst, kann man dann ihre Bewegung vorausberechnen? Kann es zum Beispiel periodische Bahnen geben? In der Tat kann diese Frage ganz schön schwierig sein, vor allem, wenn man beliebige Tischformen zulässt.

Wenn man gekrümmte Banden erlaubt, kann Billard (wie auch ein Flipperkasten) sogar chaotisch werden. Unter einem chaotischen Prozess versteht man in der Theorie der dynamischen Systeme einen Prozess, bei dem das zukünftige Verhalten aufgrund unvermeidbarer Messungenauigkeiten in der Ausgangssituation kaum oder gar nicht mehr prognostiziert werden kann. Eine solche sensitive Abhängigkeit von den Anfangsbedingungen weist das Wetter ebenso auf wie etwa das Gerät zur Ziehung der Lottozahlen oder ein System aus drei oder mehr Himmelskörpern. Schon allergeringste Änderungen in den Anfangsbedingungen führen schliesslich zu völlig anderen Entwicklungen. Oft bezeichnet man dieses Verhalten auch als «Schmetterlingseffekt».

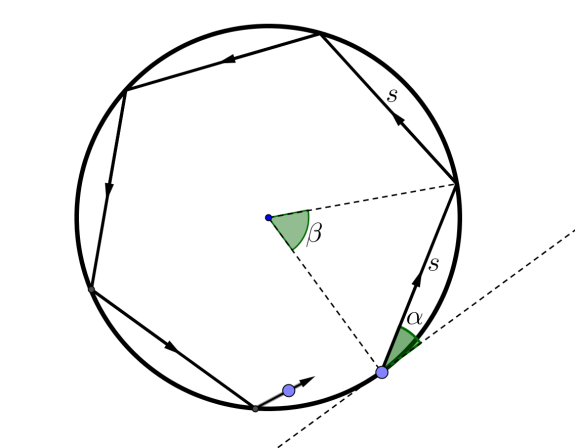
Einfacher und übersichtlicher wird alles, wenn wir die Frage etwas einengen: Gibt es auf einem kreisförmigen Billardtisch periodische Bahnen? In der Abbildung haben wir eine punktförmige Kugel irgendwo am Rand positioniert und stossen sie nun unter einem Winkel α zur Kreistangente an. Wird sie – wenn überhaupt – jemals zum Ausgangspunkt zurückkehren? Nun, mit etwas Geometrie sieht man schnell, dass die Bahnstücke zwischen den Reflexionen immer gleich lang sein müssen (in der Abbildung mit s bezeichnet) und dass ein Zentriwinkel β gerade doppelt so gross wie α ist. Soll die Bahn der Kugel also periodisch sein, dann muss der Zentriwinkel β entweder in 360° oder in einem Vielfachen davon restlos aufgehen. Anders gesagt: Das Verhältnis aus dem Anstosswinkel und 180° muss rational sein.

Frage: Was für eine wohlbekannte Bahn wird die Kugel auf unserem kreisförmigen Tisch vollführen, wenn wir sie unter einem Winkel von 72° zur Tangente anstossen?

Armin P. Barth ist Gymnasiallehrer an der Kantonsschule Baden und Autor. Die Lösung erscheint am nächsten Dienstag auf der Seite Leben&Wissen.