„Die Verführung, die von einem Beweis ausgeht, ist zu groß. Ihr erliegen die meisten, auf die Dauer alle“, lässt Bertold Brecht seinen Protagonisten Galileo Galilei im Stück „Leben des Galilei“ sagen. Das traf zwar damals nicht zu: Die Hofbeamten des erst 9jährigen Grossherzogs von Florenz, Cosmo de Medici, weigerten sich, durch Galileis Fernrohr in die Gestirne zu schauen, wo sie den Beweis für Galileis Behauptungen tatsächlich hätten erleben können. Stattdessen suchten sie einen theoretischen Disput, in dem Aristoteles‘ Autorität nie angezweifelt werden durfte. Aber heute wird sich wohl niemand ernstlich einem wirklich überzeugenden Beweis verschliessen. Darum wollen wir hier wieder einmal einen Beweis wagen.

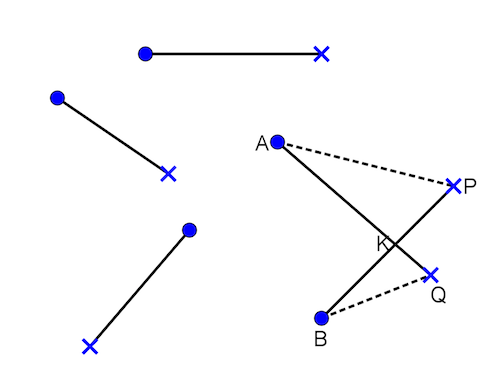
Wir behaupten Folgendes: Angenommen, es sind n Häuser (die Punkte in der Abbildung) und ebenso viele Brunnen (die Kreuze) gegeben und zwar so, dass keine drei dieser Objekte auf einer Geraden liegen. Dann kann man immer, völlig unabhängig davon, wie die Häuser und Brunnen angeordnet sind, jedes Haus mit einem Brunnen so durch eine Leitung verbinden, dass sich keine zwei Leitungen kreuzen. Die durchgezogenen Linien in der Abbildung zeigen solche Leitungen, aber wir haben da doch noch eine Kreuzung eingebaut, die es ja eigentlich zu verhindern gilt.

Warum ist das so? Ein Beweis schafft Klarheit: Zunächst gibt es sicher nur endlich viele Möglichkeiten, jedes Haus mit je einem Brunnen zu verbinden. (Wie viele übrigens?) Unter diesen endlich vielen Varianten können wir sicher eine auswählen, in der die Gesamtlänge aller Leitungen minimal ist, also unmöglich weiter verkleinert werden kann. Eine solche Konstellation besteht automatisch aus sich nicht überkreuzenden Leitungen! Warum? Gäbe es doch noch eine Überschneidung wie in der Abbildung, so könnte man durch eine Neuanordnung der Leitungen (die gestrichelten Linien) die Gesamtlänge verkürzen. Es wäre dann nämlich

AP + BQ < (AK + KP) + (BK + KQ) = AQ + BP

Aber das wäre ein Widerspruch zu der Annahme, dass die Gesamtlänge aller Leitungen minimal sein soll. Folglich kann es bei der minimalen Konstellation keine Überschneidungen mehr geben. Und der Beweis ist vollbracht.

Spüren Sie in sich die Verführung, die von diesem Beweis ausgeht? Und dass Sie bereit sind, ihm zu erliegen? Vielleicht möchten Sie selber einen ähnlichen Beweis versuchen. Hier ist eine Behauptung: Denken wir uns einen Bogen Häuschen-Papier, aber der Bogen ist theoretisch unbegrenzt, geht also auf alle Seiten endlos weiter. Jemand hat in jedes Häuschen eine positive ganze Zahl hineingeschrieben und zwar so, dass die Zahl in jedem Häuschen gleich dem Durchschnitt der vier daran angrenzenden Nachbar-Häuschen ist. Können Sie beweisen, dass dann zwingend alle Zahlen gleich sein müssen?

Armin P. Barth ist Gymnasiallehrer an der Kantonsschule Baden und Autor. Die Lösung erscheint am nächsten Dienstag auf der Seite Leben&Wissen.