Rundgänge haben in der Mathematik eine lange Tradition. Im frühen 18. Jahrhundert hat Leonhard Euler nachgewiesen, dass in der Stadt Königsberg (heute Kaliningrad) kein (geschlossener) Rundgang möglich war, bei dem jede der damals sieben Brücken über den Fluss Pregel genau einmal benutzt wird. Die Beweisführung, die er benutzt hatte, hat in der Folge zwei Gebiete befeuert, die heute aus der Mathematik nicht mehr wegzudenken sind: die Graphentheorie und die Topologie. Im Jahr 1930 tauchte erstmals ein Rundgang-Problem auf, das unter dem Titel „Problem des Handlungsreisenden“ Interesse weckte. Es geht darum, einen Rundgang durch eine Menge von Städten so zu finden, dass der Gesamtweg minimale Länge aufweist. Die Fragestellung hat zahlreiche praktische Anwendungen, so etwa in der Tourenplanung, in der Logistik oder im Design von Mikrochips. Leider ist das Problem in den Siebzigerjahren des 20. Jahrhunderts als NP-vollständig erkannt worden, was ungefähr bedeutet, dass kein Computerprogramm gebaut werden kann, welches einen optimalen Rundgang in jedem Fall in vernünftiger Laufzeit finden kann.

Das Rundgangproblem, dem wir uns heute widmen wollen, ist 1988 von Lee Sallows, einem Ingenieur, erfunden worden. Um es zu verstehen, versetzen wir uns in Gedanken in eine Stadt, deren Strassen in einem perfekten Schachbrettmuster angeordnet sind. Wir sind eingeladen, einen Rundgang nach folgender Regel zu finden: Wie gehen zuerst einen Strassenblock nach Norden, dann wenden wir uns entweder nach Westen oder Osten und gehen 2 Blocks weiter. Dort angekommen, wenden wir uns nach Süden oder Norden und gehen 3 Blocks weiter. So fahren wir immer fort; wir wechseln also immer von der Nord-Süd-Richtung in die West-Ost-Richtung und umgekehrt und gehen jedes Mal einen Block weiter als vorher. Wir müssen aber dafür sorgen, dass wir irgendwann wieder am Startpunkt ankommen. Wenn wir eine solche Tour „eckigen Rundgang“ nennen, so stellt sich sofort eine erst Frage: Gibt es überhaupt eckige Rundgänge?

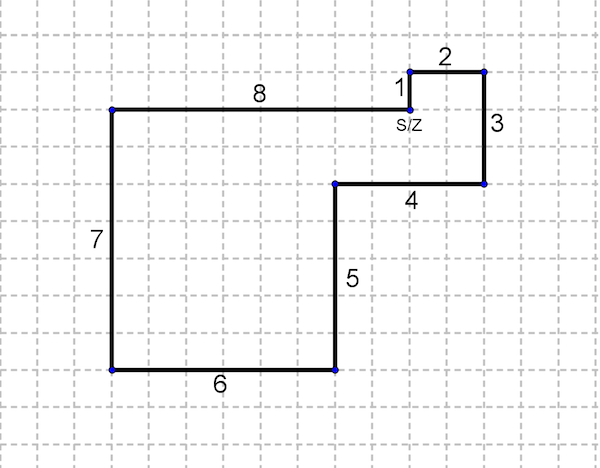
Ein Blick auf die Abbildung beantworte diese Frage sofort mit ‚ja‘. Interessanter ist also die Frage, was für Eigenschaften ein eckiger Rundgang hat. Zunächst ist schnell klar, dass jeder eckige Rundgang aus einer geraden Zahl von Strecken bestehen muss. Die erste Strecke hat ja Länge 1 (eine ungerade Zahl) und zeigt in Nord-Richtung. Überhaupt gehen alle Strecken ungerader Länge in Nord-Süd-Richtung und alle Strecken gerader Länge in West-Ost-Richtung. Da die letzte Strecke in West-Ost-Richtung laufen muss, kann es sich nur um eine gerade Zahl handeln.

Können Sie, geschätzte Leserinnen und Leser, zeigen, dass die Anzahl Strecken einer eckigen Rundreise sogar durch 4 teilbar sein muss? Martin Gardner hat bewiesen, dass die Anzahl Strecken sogar durch 8 teilbar sein muss und – mehr noch – dass zu jeder durch 8 teilbaren Zahl mindestens eine eckige Rundreise mit dieser Streckenzahl existieren muss. Wie kann man das wohl einsehen?

Armin P. Barth ist Gymnasiallehrer an der Kantonsschule Baden und Autor. Die Lösung erscheint am nächsten Dienstag auf der Seite Leben&Wissen.