Am 8. August 1900 hielt der renommierte deutsche Mathematiker David Hilbert anlässlich des Internationalen Mathematik-Kongresses in Paris einen Vortrag, der grosse Wellen schlagen sollte. Er stellte 23 mathematische Probleme vor, die damals noch ungelöst waren und von deren Bearbeitung er sich einen starken Entwicklungsschub in der mathematischen Forschung erhoffte. Dieser Plan ging tatsächlich auf. Hilberts Bekanntheit war es zu verdanken, dass zahlreiche Forscherinnen und Forscher sich sofort an die Arbeit machten und viel Energie in die Untersuchung der Probleme lenkten. Wenn dabei auch nicht immer die Ergebnisse erzielt wurden, die sich Hilbert erhofft hatte, so wurden diverse Teilgebiete der Mathematik doch stark vorangetrieben und ungeheuer bereichert.

Das Problem Nummer 10 zum Beispiel verlangte, ein Verfahren zu entwickeln, mit dem sich entscheiden lässt, ob eine Diophantische Gleichung lösbar ist oder nicht. Das ist ein spezieller Typ Gleichung, bei dem ausschliesslich ganzzahlige Lösungen gesucht werden. Die Gleichung x2+y4=–3 etwa hat sicher keine Lösung, weil die linke Seite niemals negativ werden kann. Die Gleichung x-y2=0 dagegen ist lösbar: Zum Beispiel kann man für x 4 und für y 2 einsetzen oder man kann für x 9 und für y 3 einsetzen oder aus unendlich vielen weiteren Einsetzungen wählen. Im Jahr 1970, also knapp 30 Jahre nach Hilberts Tod, hat Juri Matijasewitsch beweisen können, dass kein solches Verfahren existieren kann, wie clever man es auch anstellen mag.

Im Jahr 2000 versuchte das Clay Mathematics Institute, einen ähnlichen Entwicklungsschub in der mathematischen Forschung zu erzeugen, wie es Hilbert 100 Jahre zuvor getan hatte. Das Institut definierte sieben sogenannte Millennium-Probleme und schrieb zur Lösung von jedem einzelnen ein Preisgeld von einer Million US-Dollar aus. Das einzige seither gelöste Millennium-Problem ist die Poincaré-Vermutung; diese wurde 2002 von Grigori Perelman gelöst. Die Fields-Medaille, die ihm dafür verliehen werden sollte, lehnte er allerdings ebenso ab wie das Preisgeld. Die Lösung der restlichen Probleme ist immer noch ausstehend.

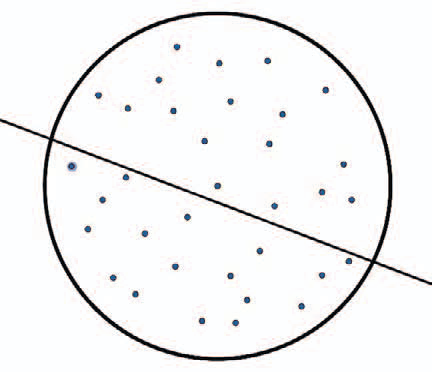
Nun bietet die Mathematik nebst schwergewichtigen Problemen der erwähnten Art auch unzählige viel einfachere Probleme, die jeden erfreuen mag, der gerne intensiv über mathematischen Rätseln brütet. Hier ist ein solches Problem: Denken wir uns einen Kreis, in dem 100‘000 Punkte völlig zufällig gewählt worden sind. (Die Abbildung zeigt der besseren Übersicht zuliebe deutlich weniger Punkte.) Die Frage ist nun: Ist es möglich, eine Gerade so durch den Kreis zu legen, dass genau 50‘000 Punkte auf der einen und 50‘000 Punkte auf der anderen Seite der Gerade zu liegen kommen? Ist das immer möglich, ganz egal, wie die Punkte im Kreis verstreut sind? Kann man ein Verfahren finden, mit dem man in jedem nur denkbaren Fall eine solche Trenngerade finden kann?

Armin P. Barth ist Gymnasiallehrer an der Kantonsschule Baden und Autor. Die Lösung erscheint am nächsten Dienstag auf der Seite Leben&Wissen.