

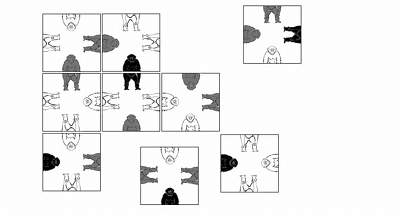
IM HANDEL ist ein Spiel erhältlich, welches aus neun quadratischen Kärtchen besteht, die zu einem grossen Quadrat zusammengefügt werden müssen (vgl. Abbildung). Die Schwierigkeit besteht darin, die Kärtchen so hinzulegen, dass an jeder Kante, in welcher zwei Kärtchen zusammenstossen, ein vollständiger und einfarbiger Affe entsteht. Das Rätsel ist interessant und herausfordernd – und mit einigem Aufwand durchaus lösbar. Aber nehmen wir einmal an, jemand schenkt Ihnen ein Affenpuzzle aus 25 Kärtchen, die folglich zu einem 5-mal-5-Quadrat zusammengefügt werden müssen. Sollten Sie dem Schenker dankbar sein?
Nein, keineswegs. Sie sollten ihn verfluchen und das Geschenk ablehnen, denn Sie gingen wahrscheinlich daran zugrunde. Rechnen wir einmal nach, wie viele Möglichkeiten es gibt, die Kärtchen in einem Quadrat anzuordnen. Für die Ecke unten links haben Sie 25 mögliche Kärtchen zur Auswahl. Haben Sie sich für eines entschieden, so bleiben 24 Möglichkeiten, dem Eckkärtchen rechts ein weiteres Kärtchen anzufügen. Also gibt es schon 25 mal 24 gleich 600 Varianten, die beiden ersten Kärtchen hinzulegen. Für jede dieser Varianten gibt es 23 Möglichkeiten, das dritte Kärtchen der untersten Zeile zu platzieren, womit wir schon bei 13 800 Varianten angelangt sind. Zur Komplettierung des gesamten 5-mal-5-Quadrates müssten Sie also alle Zahlen von 25, über 24, 23, 22, 21 und so weiter bis hinunter zu 1 miteinander multiplizieren. In der Mathematik nennt man das die Fakultät von 25.
Aber damit nicht genug. Da man jedes Kärtchen auch noch auf vier Arten ausrichten kann, müssen Sie das riesige Resultat der obigen Rechnung 25-mal mit 4 multiplizieren. Dabei entsteht eine Zahl, die so unfassbar gross ist, dass Sie schlagartig der Mut verlassen wird, dieses Puzzle auch nur anzurühren. Aber vielleicht kommt Ihnen die Idee, alle Varianten von einem Computer rechnen zu lassen. Doch dagegen spricht, dass das Affenproblem NP-vollständig ist. Das bedeutet, dass es bis heute keinem Menschen geglückt ist, ein wirklich schnelles Computerprogramm dafür zu entwickeln und, mehr noch, dass in dem Moment, wo das jemandem glücken sollte, schlagartig über tausend andere NP-vollständige Probleme, für die bis heute kein effizientes Lösungsverfahren bekannt ist, effizient lösbar wären. Und ebendies ist extrem unwahrscheinlich. Dennoch könnte man der Meinung sein, dass ein Computer aufgrund seiner immensen Rechenleistung in der Lage sein sollte, alle Varianten in vernünftiger Zeit zu überprüfen. Oder etwa nicht?
Angenommen, es steht Ihnen ein Computer zur Verfügung, der pro Sekunde eine Milliarde Varianten errechnen und testen kann, was überaus optimistisch ist. Wie lange würde diese Maschine dann im Mittel rechnen, um die korrekte Anordnung der 25 Kärtchen zu finden?
Armin P. Barth ist Gymnasiallehrer an der Kantonsschule Baden und Autor.
Die Lösung erscheint auf der Leserbriefseite vom Montag, 4. November 2013.