EISENBAHNNETZE. «Baut keine Festungen, baut Eisenbahnen!» soll Helmuth Bernhard Graf von Moltke (1800– 1891) einmal gesagt haben. Der Generalfeldmarschall muss ein begnadeter Stratege gewesen sein, denn er war an einigen preussisch-deutschen Siegen massgeblich beteiligt. Zuvor hatte Preussen Militärbeobachter in den amerikanischen Bürgerkrieg gesandt, die auf der Seite der Nordstaaten den Sezessionskrieg mitverfolgt und dann zu Hause von den «Segnungen» der modernen Kriegsführung berichtet hatten, der Eisenbahn und dem Telegrafen. Es ist klar: Dank Eisenbahnen lassen sich Truppenverschiebungen in viel kürzerer Zeit realisieren, und gegen die Telegrafen waren die alten Meldereiter chancenlos. Moltke zog seine Lehren aus diesen Beobachtungen rasch und drängte darauf, alle Energie in Eisenbahnnetze zu stecken und nicht mehr in den Bau von Festungen.

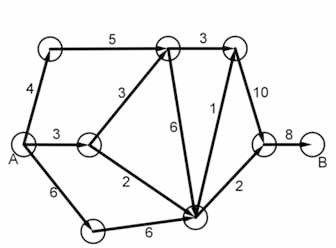
Eisenbahnnetze spielten auch eine grosse Rolle in den beiden Weltkriegen. Und als später die Computer erfunden wurden, gab es Bemühungen seitens der USA, das sogenannte Problem des maximalen Flusses elektronisch zu bewältigen. Dieses Problem fragt danach, welches die maximale Anzahl Züge ist, die von A nach B über ein bestehendes Netzwerk von Transportwegen (Schienen) gelangen können? Das ist ein mathematisches Problem, und es wurde 1956 gelöst von L. R. Ford und D. R. Fulkerson. Die beiden Forscher fanden einen Algorithmus (ein automatisierbares Verfahren), mit dem sich zu jedem beliebigen Netzwerk der maximale Fluss finden lässt, der von A nach B führt. Betrachten wir einmal das Netzwerk in der Abbildung (oben). Die Pfeile können Transportwege jeder Art sein, Schienen, Strassen, Seerouten und so weiter. Wir können uns das auch als Röhrensystem vorstellen, in dem nun möglichst viel Wasser von A nach B fliessen soll. An jedem Pfeil ist dessen Kapazität angegeben; das ist die maximale Wassermenge (die maximale Anzahl Züge), die pro Zeiteinheit auf diesem Weg oder durch diese Röhre befördert werden kann. Es ist sofort klar, dass der maximale Fluss beschränkt ist durch die Summe der Kapazitäten derjenigen Pfeile, die A verlassen, also 4+3+6=13 im abgebildeten Beispiel. Die interessante Frage ist nun aber, ob der ganze Rest des Netzwerks diesen Fluss auch «schlucken» kann. Dabei müssen wir uns einfach an die naheliegende Forderung halten, dass bei jedem Verzweigungspunkt die Summe der einfliessenden Mengen gleich der Summe der ausfliessenden Mengen sein muss. Welchen maximalen Fluss, welche Gesamtliterzahl an Wasser können wir also bei A einspeisen, damit das Netzwerk den Fluss schlucken und bis zu B transportieren kann? Können Sie das beantworten? – Ford und Fulkerson hatten eine tolle Idee! Sie suchten nach sogenannten Schnitten. Ein Schnitt ist eine Menge von Röhren, durch die der ganze Fluss hindurch muss und die aber insgesamt eine möglichst kleine Gesamtkapazität haben, nach dem Motto: Wenn ich den engsten Engpass finde, kenne ich auch den maximalen Fluss. Moltke hätte bestimmt seine helle Freude an dieser Idee gehabt …

Die Lösung erscheint mit seiner nächsten Kolumne am Dienstag, 4. Dezember 2012.

Lösung vom 2. Oktober 2012: x·50%+y·50%+z·100%=(x+y+z)·50%+- z·50%=1·50%+z·50%!