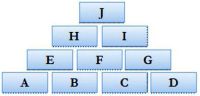
ZAHLENMAUER. Ein mit mir befreundeter Mathematiker hält Zahlenmauern für ein überaus nützliches Werkzeug, um sich mit einigen Konzepten vertraut zu machen, die in der Mathematik eine zentrale Rolle spielen. Da kann ich nur zustimmen. Eine Mauer wie die abgebildete eröffnet allerlei interessante Fragen. Dazu muss man lediglich wissen, welchem Bildungsgesetz die Mauer gehorchen muss: Der Wert jedes Backsteins ist die Summe der Werte der beiden unter ihm liegenden Steine.

Hat also zum Beispiel A den Wert 7 und B den Wert 4, so hat E den Wert 11, die Summe aus 7 und 4. Indem wir nun von einigen Steinen den Wert vorgeben und von anderen den Wert erfahren möchten, entstehen zahlreiche aufschlussreiche Aufgaben. Beispiele gefällig?
Zuerst nehmen wir an, die Werte der Steine A, B, C und D seien bekannt und der Wert von J sei gesucht. Das schaffen wir leicht: J ist ja die Summe von H und I. Und da H die Summe von E und F und I die Summe von F und G ist, folgt, dass J = E + 2F + G ist. E wiederum ist die Summe von A und B, F ist die Summe von B und C, und G ist die Summe von C und D. Setzen wir alles zusammen, so finden wir J = A + 3B + 3C + D. Damit haben wir eine Formel für J gewonnen. Wann immer also die vier untersten Steine bekannt sind, können wir damit den Wert des obersten Steins (und natürlich auch die Werte aller anderen Steine) berechnen. Problem gelöst. Nehmen wir nun an, A, C, D und J seien bekannt, etwa A = 4, C = 2, D = 1 und J = 17. Können wir daraus B berechnen? Nichts leichter als das: Die Mauer offeriert uns ja die Gleichung J = A + 3B + 3C + D, in der einzig B unbekannt ist. Wir brauchen also nur die Gleichung 17 = 4 + 3×B + 3×2 + 1 nach B aufzulösen und erhalten B = 2. Eine Gleichung spricht immer eine Frage aus: Welchen Wert muss B haben, damit die beiden Seiten übereinstimmen? Gleichungen haben in der Mathematik eine enorme Bedeutung, nur leider gelingt die Lösung nicht immer so leicht und geradlinig wie eben. Ändern wir zum Beispiel J zu 16 ab und lassen A, C, D wie vorher, so entsteht die Lösung B = 5/3. Falls es Gründe dafür gäbe, nur ganze Zahlen zu akzeptieren, müsste unser Urteil somit lauten, dass die Gleichung keine Lösung besitzt. Ob eine Gleichung also Lösungen besitzt oder nicht, hängt oft auch davon ab, was wir als Lösungen überhaupt zulassen wollen und können.

Angenommen, es wären einzig A = 4, C = 2 und J = 20 bekannt. Können wir die restlichen Steine dann berechnen? Nun, bezüglich der Werte der Steine B und D wissen wir einzig, dass 4 + 3×B + 3×2 + D = 20 oder – vereinfacht – dass 3B + D = 10 ist. Diese Information reicht einfach nicht aus. Die Gleichung hat zwei Unbekannte und darum keine eindeutige Lösung mehr. Zum Beispiel würden B = 0 und D = 10 die Gleichung erfüllen, aber auch B = 1 und D = 7 oder B = 2 und D = 4 oder B = 3 und D = 1, und wenn wir beliebige Zahlen zulassen, gibt es unendlich viele Lösungen.

Wieder eine andere Frage stellt uns die Mauer, wenn wir A = 5, D = 1, H = 22 und I = 26 vorgeben.

Können Sie daraus B und C bestimmen?

Die Lösung erscheint mit der nächsten Kolumne am 7. August 2012

Lösung vom 5. Juni 2012: 13 Holzfäller, 83 Stoffballen