IM HERBST 1654 geschah ein folgenschwerer Unfall: Das Pferd, das seine Kutsche zog, schlug ausgerechnet auf einer Brücke aus. Darauf kippte die Kutsche über das Brückengeländer, so dass der Fahrgast angsterfüllt an den Seilen über dem gurgelnden Wasser hing.

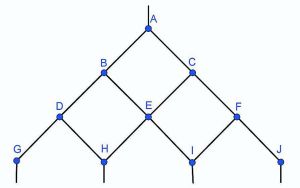
Obwohl er gerettet wurde, soll dieses Ereignis das Leben des französischen Mathematikers Blaise Pascal stark verändert haben. Es ist allerdings mehr als fraglich, ob es sich überhaupt so zugetragen hatte. Zu vermuten ist, dass irgendein einschneidendes Erlebnis dem Leben des erst 31-jährigen Pascal fortan eine ganze andere Richtung gab. Ab dem Jahr 1654 zog er sich jedenfalls vollständig aus der Pariser Gesellschaft zurück, um sich fortan dem Verfassen religiöser Schriften zu widmen, die teilweise so wirkungsvoll waren, dass sie sogar den Beginn des Niedergangs der französischen Jesuiten einleiteten. Kurz zuvor aber hatte Blaise Pascal noch grossartige Mathematik erschaffen. Geniessen wir einmal ein kleines Stück davon: Stellen wir uns dazu vor, wir hätten eine Art Röhrensystem vor uns, in das wir ganz oben eine kleine Kugel einwerfen. Die Kugel bahnt sich nun ihren Weg bis ganz nach unten, wobei an jeder Gabelung der Zufall entscheidet, ob sie nach links oder nach rechts rollt. Um zur Stelle A zu gelangen, gibt es offenbar nur einen einzigen Weg, nämlich durch das oberste Röhrchen. Merken wir uns also die Zahl 1. Um zur Stelle B oder C zu gelangen, gibt es auch nur je einen Weg, nämlich, indem die Kugel bei A nach links bzw. nach rechts abzweigt. Merken wir uns also die Zahlen 1, 1.

Auch nach D und F gibt es nur je einen Weg; nach E aber führen zwei Wege, einer über B, der andere über C. Merken wir uns auch diese drei Zahlen: 1, 2, 1.

Wie viele Wege führen nach H? Nun, da es einen Weg nach D und zwei Wege nach E gibt und H nur über diese zwei Stellen erreicht werden kann, muss es folglich 1 + 2 = 3 Wege nach H geben. Um zu Zahlen der nächsttieferen Schicht zu gelangen, genügt es offenbar, diejenigen beiden Zahlen der darüberliegenden Schicht zu addieren, über die die Wege nur führen können. Für die Stellen G–J erhalten wir somit die Zahlen 1, 3, 3, 1. So fortfahrend, erhält man das so genannte Pascal-Dreieck, das in vielen mathematischen Anwendungen eine wichtige Rolle spielt.

Fragen wir uns etwa Folgendes: Beim Spiel Euro Millions muss man zwei von elf Sternchen markieren; wie viele Möglichkeiten hat man dazu? Dazu denken wir uns ein Röhrensystem aus 11 Schichten, 1 pro Sternchen. Die Abzweigung nach links zu wählen, bedeutet, dieses Sternchen zu markieren, nach rechts, es nicht zu markieren.

Da genau zwei Sternchen zu markieren sind, interessieren uns alle Wege, bei denen die Kugel genau zweimal nach links und neunmal nach rechts rollt. An welche Stelle im Pascal-Dreieck gelangt man so? Und vor allem: Welche Zahl steht dort?

Die drei Schnellsten, die die Lösung dieser Kolumne wissen, erhalten das neue Buch von Armin Barth: Lösungszahl mit Adresse an: claudia.weiss@azmedien.ch