IM JAHR 1973, anlässlich einer Mathematik- Konferenz, stellte Victor Klee einem jüngeren Kollegen ein interessantes Problem. Der Kollege, der 1946 in Prag geborene Vašek Chvátal, löste das Problem schnell. Später kamen Mathematiker auf noch einfachere Lösungen.

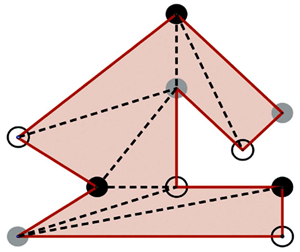
Das Problem lautet: Wir denken uns den Grundriss eines Museums als beliebiges Vieleck (siehe Abbildung). Da sich beim Bau moderner Museen oft renommierte Architekten austoben, sind ungewöhnliche, verwinkelte Formen keine Seltenheit. Zur Bewachung der Ausstellungsstücke denken wir uns Wächter in einigen Ecken des Raums positioniert, und wir fragen uns, wie viele Wächter nötig sind, um den ganzen Ausstellungssaal lückenlos zu überwachen? Genauer: Wenn das Museum x Ecken beziehungsweise x Wände aufweist, wie viele Wächter reichen dann, egal, welche Form der Saal hat, immer aus, damit jeder Punkt des Saals von mindestens einem Wächter überblickt werden kann?

Diese Frage hat praktische Anwendungen, etwa in der Robotik, in der Computergrafik oder bei der Optimierung von Sensornetzwerken. Die Lösung ist an Eleganz kaum zu überbieten: Zunächst lässt sich der Grundriss immer triangulieren. Das bedeutet, dass durch Einfügen von geradlinigen Verbindungen von Eckpunkten (die gestrichelten Linien) die Figur in lauter nicht überlappende Dreiecke unterteilt wird. Das ist auf mehrere Arten möglich.

Nach erfolgter Triangulation können wir die Eckpunkte dreifärben. Das bedeutet, dass alle Eckpunkte mit insgesamt drei Farben (hier weiss, grau und schwarz) so eingefärbt werden, dass nie zwei durch eine Linie direkt verbundene Ecken dieselbe Farbe aufweisen. Offenbar kommt dann in jedem Dreieck jede der drei Farben genau einmal vor, und es ist leicht einzusehen, dass eine solche Dreifärbung immer möglich ist. Positionieren wir in unserem 10-eckigen Museum nun vier Wächter in den weissen Ecken, so ist der ganze Raum überwacht, weil jedes Dreieck eine weisse Ecke hat. Allerdings kann eine erfolgreiche Überwachung sogar mit nur drei Wächtern erfolgen, die in den schwarzen (oder grauen) Punkten platziert werden, weil auch jedes Dreieck eine schwarze Ecke hat. Allgemein findet man also die in jedem Fall ausreichende Anzahl Wächter, indem man die Anzahl Ecken (hier 10) durch 3 teilt und das Resultat abrundet. Denn so viele Ecken der seltensten Farbe gibt es. Damit ist das Problem gelöst.

Übrigens: Aus wie vielen Dreiecken besteht eigentlich die Triangulation eines Vielecks aus x Ecken? Und ist diese Anzahl abhängig von der konkreten Art der Triangulation?

Lösung vom 5. Juli 2011: Suche den Bruch mit der grössten Zweierpotenz im Nenner. Beim Erweitern ist dies der einzige, dessen Zähler nicht mit mindestens einem Faktor 2 multipliziert wird.