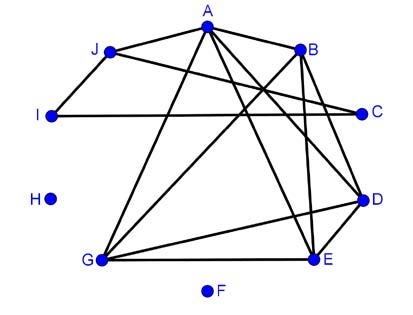
Eine Schulklasse wurde gebeten, aus einer Liste von möglichen Freifächern auszuwählen; dabei konnte jeder Schüler und jede Schülerin ganz nach Belieben keines, eines oder mehrere Freifächer ankreuzen. So ist die Abbildung entstanden: Jeder Punkt repräsentiert eines der Freifächer A – J, und ich habe zwei Punkte immer dann durch eine Linie verbunden, wenn diese beiden Freifächer zur gleichen Zeit stattfinden können, was natürlich daran liegt, dass sich niemand für beide Fächer eingeschrieben hat.

Da die Freifächer neben dem regulären Unterricht Platz haben müssen, ist es erstrebenswert, ihre Stundensumme so tief wie möglich zu halten. Das heisst, wir müssen daran interessiert sein, in der Abbildung so viele Punkte wie möglich zu finden, von denen jeder mit jedem verbunden ist. Die Freifächer einer solchen Gruppe könnte man nämlich alle gleichzeitig stattfinden lassen und damit die Stundensumme aller Freifächer relativ niedrig halten.

Die hier beschriebe Fragestellung ist in der Mathematik sehr häufig. Sie zählt zur Graphentheorie, weil Mathematikerinnen und Mathematiker eine Menge von Punkten, von denen einige mit einigen durch Linien verbunden sind, einen Graphen nennen. Was wir hier anstreben, ist, im Graphen eine möglichst grosse Gruppe von Punkten zu finden, von denen jeder mit jedem verbunden ist, und eine solche Menge von Punkten nennt man Clique.

Menschen, die der Mathematik gegenüber negative Gefühle hegen, könnten jetzt einwenden, das sei ja eine furchtbar abstrakte Fragestellung, die mit der Welt wenig zu tun habe. Aber solchen Menschen können wir – nicht ohne Genuss – entgegnen, dass die Aufgabe, möglichst grosse Cliquen in Graphen zu finden, zwar in einem abstrakten Gewand daher kommt, dass sie gerade deswegen aber in besonders vielen realen Situationen anwendbar ist.

Die Punkte könnten zum Beispiel die Teilarbeiten eines komplexen Fertigungsprozesses darstellen, und wir verbinden zwei Punkte genau dann, wenn beide zur selben Zeit ausgeführt werden können. Die grösstmögliche Clique liefert dann eine Gruppe von Teilarbeiten, die alle parallel ausgeführt werden können. Oder wir stellen uns die Punkte als mögliche Übergänge einer komplizierten Strassenkreuzung vor, und wir verbinden zwei Punkte genau dann, wenn die beiden Übergänge gleichzeitig auf Grün geschaltet werden können. Dann liefert die grösstmögliche Clique die maximale Menge von Kreuzungsübergängen, die alle parallel offen sein dürfen, ohne dass Fahrzeuge einander in die Quere kommen. In beiden Fällen entspricht die Suche nach Cliquen einem plausiblen und praktischen Interesse.

Leider ist das Cliquenproblem NP-vollständig, was bedeutet, dass es sehr wahrscheinlich kein effizientes Verfahren gibt, das bei allen Graphen erfolgreich ist. Immerhin können Sie, liebe Leserinnen und Leser, sicher das abgebildete Problem lösen: Wenn jedes Freifach eine Stunde dauert, was ist dann die kleinste Zahl an Stunden, in denen alle Fächer A – J untergebracht werden können?

Lösung vom 3. Mai 2011: 107 erfüllt die Eigenschaft mit der Nummer 107 genau dann, wenn sie sie nicht erfüllt.