Glaubt man Vergils Schilderungen in seiner Aeneis, so muss sich um 900 v. Chr. an der Nordküste Afrikas eine faszinierende Geschichte zugetragen haben: Die phönizische Prinzessin Dido verliess ihr Land fluchtartig, nachdem ihr Ehemann von König Pygmalion ermordet worden war. Die Flucht brachte sie an diejenige Stelle Afrikas, an der später Karthago erblühen sollte. Sei es nun aus List oder aus Bescheidenheit, jedenfalls erbat Dido vom hier herrschenden König Jarbas für sich und ihre Gefolgsleute nur ganz wenig Land, nämlich so viel, wie sich mit einer Ochsenhaut umspannen lässt.

Kaum hatte Jarbas ihr seine Zustimmung und eine Ochsenhaut gegeben, zerschnitt sie die Haut in ganz dünne Streifen, knüpfte diese zu einer „Schnur“ zusammen und stand nun vor der Frage, in welche Form sie ihr Landstück bei gegebenem Umfang bringen sollte, um den grösstmöglichen Flächeninhalt zu erreichen, denn daran war ihr zweifellos gelegen.

In der Mathematik nennt man dies das isoperimetrische Problem, und es kann in vielen verschiedenen Varianten gestellt werden. Die einfachste Version entsteht, wenn wir annehmen, Dido wollte unbedingt ein rechteckiges Landstück abgrenzen. Bei einer Schnurlänge von zum Beispiel 1000 m wäre nämlich das Quadrat mit Seitenlänge 250 m die Figur mit maximaler Fläche, weil jedes nicht-quadratische Rechteck mit den Seitenlängen 250 + x und 250-x die Fläche (250 + x) · 250 - x) = 250² - x², also eine kleinere Fläche als das Quadrat, hätte. Schon schwieriger ist das Problem, wenn wir annehmen, Dido hätte auf einem dreieckigen Landstück bestanden. Es ist beweisbar (allerdings nicht mehr so einfach), dass unter allen Dreiecken gleichen Umfangs das gleichseitige den grössten Flächeninhalt hat.

Am schwierigsten wird das Problem, wenn das Landstück eine beliebige Form haben kann. Erst der deutsche Mathematiker Karl Weierstrass hat im 19. Jahrhundert lückenlos beweisen können, dass es in diesem Fall der Kreis ist, der das Problem löst. Viele Erbauer mittelalterlicher Städte (wie etwa Köln) wussten das intuitiv, als sie die an Flüssen errichteten Städte mit halbkreisförmigen Schutzmauern umschlossen, um so bei gegebener Mauerlänge ein Maximum an Fläche herauszuholen. Und die Natur führt uns die Lösung des allgemeinen isoperimetrischen Problems immer wieder vor Augen, wenn wir Seifenblasen betrachten, diese Häute kleinsten Flächeninhalts, die eine gewisse Menge an Sauerstoff einschliessen.

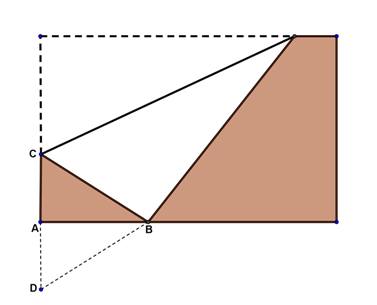
Möchten Sie selber eine Aufgabe lösen, die dieses überaus wichtige Prinzip benutzt? Bitteschön: Legen Sie ein Blatt Papier im Querformat vor sich hin und falten sie die linke obere Ecke irgendwo auf die untere Längskante. Wie genau muss man diese Faltung ausführen, damit das Dreieck ABC den grösstmöglichen Flächeninhalt hat? Ich habe schon etwas geholfen, indem ich C an AB gespiegelt habe…

Lösung von 13. Juli 2010: Die Strecke HQ hat Länge √2 . Wir gehen also von H aus 3 Einheiten nach rechts und dann die Länge der Strecke HQ nach oben.