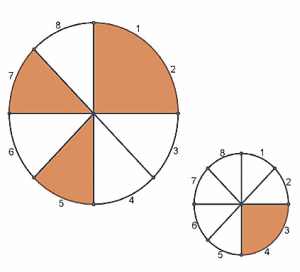
MATHEMATIKER sind merkwürdige Leute. Oft werden sie als zerstreut oder abwesend beschrieben. Albert Einstein bestätigte das Vorurteil, indem er in Princeton mehrmals Passanten nach seinem eigenen Heimweg fragen musste, und 1916 gestand er in einem Brief an seinen Sohn: «Die kuriose Unterschrift in meinem letzten Schreiben ist dadurch zu erklären, dass ich öfter in meiner Zerstreutheit statt als mich selber als die Person unterschreibe, an die der Brief gerichtet ist.» Ich glaube ja, dass dieses Vorurteil ganz ungerechtfertigt ist. Wenn Mathematiker zerstreut wirken, so sind sie in Wahrheit unglaublich fokussiert und konzentriert. Auf ein Problem nämlich, das sie in Gedanken wälzen. Vielleicht erging es Ihnen, liebe Leser, ebenso, falls Sie über das Problem in der kleinen Konditorei nachgedacht haben. Hier die Auflösung: Wenn man den kleinen Schokokuchen so, wie er abgebildet ist, konzentrisch auf die grosse Früchtetorte legt, so ergibt sich folgendes Protokoll: 00000101, in dem jede 1 eine Übereinstimmung und jede 0 eine fehlende Übereinstimmung anzeigt. Wenn man den kleinen Kuchen um einen Sektor im Uhrzeigersinn weiterdreht, ergibt sich dieses neue Protokoll: 01011010. Wenn wir so fortfahren und den Schokokuchen immer um einen Sektor weiterdrehen, ergeben sich diese acht Protokolle:

0 0 0 0 0 1 0 1
0 1 0 1 1 0 1 0
1 1 1 0 0 1 0 0
1 0 0 1 1 0 0 1
0 1 1 0 0 0 1 1
1 0 0 1 0 1 1 0
0 1 1 1 1 1 0 1
1 0 1 0 1 0 1 0

DIES IST bloss ein Beispiel. Das kleine Blech darf ja beliebig viele Kuchenstücke in beliebiger Anordnung enthalten, während das grosse aber genau vier Tortenstücke enthalten muss. Wir wollen einsehen, dass es immer möglich ist, den Schokokuchen so zu drehen, dass mindestens vier Übereinstimmungen auftreten. Angenommen, es gibt bei keiner Anordnung mehr als drei Übereinstimmungen. Kann das sein? Nein, denn dann enthielte jede Zeile des obigen Zahlenschemas höchstens drei Einsen und das ganze Schema damit höchstens 8 × 3 = 24 Einsen. Ich behaupte dagegen, dass das Schema unbedingt genau 32 Einsen enthalten muss. Warum? Dazu fragen wir uns, was genau die erste Spalte des Schemas bedeutet. Sie zeigt uns, wie oft der erste Sektor des Schokokuchens bei seiner Reise rund um die Früchtetorte herum Übereinstimmung angetroffen hat. Da die Früchtetorte genau vier belegte und vier leere Sektoren aufweist, muss eine solche Übereinstimmung viermal passiert sein, einerlei, ob der erste Sektor des Schokokuchens nun belegt oder leer ist. Folglich muss die erste Spalte des Schemas genau vier Einsen enthalten und zwar völlig unabhängig davon, wie viele Kuchenstücke auf dem kleinen Blech liegen und in welcher Anordnung. Dasselbe gilt für alle anderen Spalten des Zahlschemas. Daher muss jede Spalte genau vier Einsen und das ganze Schema folglich genau 32 Einsen enthalten. Deswegen muss eine Zeile existieren, die mindestens vier Einsen enthält. Damit ist das Problem gelöst. Etwas ganz anderes: Wenn man alle natürlichen Zahlen von 1 bis und mit 132 multipliziert, auf wie viele Nullen wird dieses Produkt enden?

Die Lösung erscheint gemeinsam mit seiner nächsten Kolumne am 13. Juli 2010.