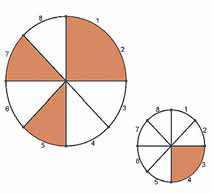
DAS SCHÖNE an der Mathematik ist, dass mathematische Probleme überall und ganz unerwartet auftauchen können. Viele sind wichtig im Hinblick auf den praktischen Nutzen. Heute soll aber einmal ein Problem vorgestellt werden, das vielleicht völlig nutzlos ist; gleichwohl ist es spannend, darüber nachzudenken, weil es eine Herausforderung ist, die sich so lange im Geiste einnistet, bis man sie gemeistert hat. Ich ging kürzlich in eine Konditorei. Während ich wartete, bis die Reihe an mir sein würde, schweifte mein Blick über die Auslage und fand Interesse an einer grossen kreisrunden Früchtetorte und einem etwas kleineren, ebenfalls kreisrunden Schokokuchen. Jeder der beiden Kuchen war in acht Stücke – Mathematiker nennen solche Stücke Sektoren – vorgeschnitten worden, und die Verkäuferin hatte offenbar schon einige Stücke ziemlich wahllos herausgenommen und verkauft. Von der Früchtetorte waren noch vier Stücke (die weissen Sektoren) und vom Schokokuchen sechs Stücke übrig. Wenn man ansteht und wartet, kommt man manchmal auf die verrücktesten Ideen. Ich hatte plötzlich den Einfall, den Schokokuchen in Gedanken auf die Früchtetorte zu legen und zu prüfen, in wie vielen Sektoren eine Übereinstimmung bestand.

DER SEKTOR 1 war beim Schokokuchen belegt, bei der Früchtetorte aber leer, also keine Übereinstimmung. Dasselbe traf für den Sektor 2 zu. Die Sektoren 3, 4, 5 und 7 enthielten entweder beim grossen Blech ein Stück Kuchen und beim kleinen nicht oder umgekehrt, also auch keine Übereinstimmung. Sektoren 6 und 8 waren bei beiden Blechen belegt, also Übereinstimmung. In Gedanken stellte ich diesen Sachverhalt durch dieses «Protokoll» dar: 000000101. Dabei bedeutete eine 1 Übereinstimmung und eine 0 keine. Die Reihenfolge der Ziffern ergab sich aus der Nummerierung der Sektoren beim Schokokuchen. Nur zwei Übereinstimmungen? Das empfand ich als mager. Daher drehte ich den kleinen Kuchen um einen Sektor im Uhrzeigersinn und legte ihn wieder auf die grosse Torte. (Nun lag also Sektor 1 des kleinen Kuchens auf Sektor 2 des grossen.) Welche Übereinstimmungen gab es diesmal?

NUN, die Antwort lautet: 01011010, wenn man wieder bei Sektor 1 des Schokokuchens anfängt. Dieses neue Protokoll zeigt schon vier Übereinstimmungen! Ich feierte innerlich diesen Erfolg, rückte in der Schlange auf und war nun gleich an der Reihe. Und in Gedanken formulierte ich diese Problemstellung: Wenn auf dem grossen Blech genau vier Sektoren belegt und vier frei sind (aber egal, in welcher Anordnung) und wenn es beim kleinen Blech völlig egal ist, wie viele Sektoren belegt sind und welche, kann man dann den Schokokuchen immer so drehen, dass es mindestens vier Übereinstimmungen gibt? Vielleicht möchten Sie, liebe Leser, darüber nachdenken, bevor Sie im Juni die Fortsetzung lesen?

Lösung der Kolumne vom 13. April: Bei 20 Städten gibt es 2×19×1× .. .×1 = 2 432 902 008 176 640 000 mögliche Routen. Ein Computer, der pro Sekunde 1 Milliarde Routen prüft, würde dafür 77 Jahre benötigen.