IN DER MATHEMATIK gibt es eine ebenso merkwürdige wie reizvolle Sammlung von Problemen. Wir nennen sie hier scherzhaft «nicht-pressierbare Probleme», kurz: NP-Probleme. (In Wirklichkeit heissen diese Probleme «NP-vollständig», und die beiden Grossbuchstaben stehen für Nicht-deterministisch Polynomial.) Das Charakteristische dieser Probleme ist, dass sie bewiesenermassen zu den härtesten Knacknüssen dieser Welt gehören in dem Sinne, dass es bis heute niemandem gelungen ist, eine schnelle, effiziente Lösung für eines dieser Probleme zu finden. (In diesem Sinne sind sie eben «nicht-pressierbar».) Aber das ist noch nicht alles: Alle NP-Probleme sind überdies untereinander verwandt, wenn auch teilweise über weite Strecken, und diese verwandtschaftlichen Bande bewirken, dass – falls jemals ein Mensch für eines dieser Probleme eine schnelle, effiziente Lösung finden sollte – gleichzeitig alle NP-Probleme schnell und effizient gelöst werden können, so als würde das familiäre Blut durch alle Verbindungen rauschen und augenblicklich alle NP-Probleme in einen anderen Status versetzen. Es gibt Hunderte solcher Probleme, und viele betreffen wichtige, praktische Gebiete. Seit dem Jahr 1993, als dem Mathematiker Aviezri Fraenkel ein Beweis dafür glückte, weiss man zum Beispiel, dass die Proteinfaltung zu dieser Sammlung der härtesten mathematischen Probleme zählt. Worum geht es dabei?

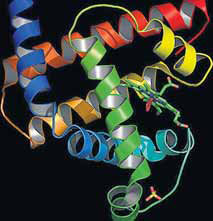
PROTEINE (oder Eiweisse) sind Moleküle, die zu den Grundbausteinen der menschlichen Zelle gehören und im Organismus viele unterschiedliche Funktionen haben. Die primäre Struktur von Proteinen ist die einer langen Perlenkette, wobei die Perlen Aminosäuren sind, deren Reihenfolge im genetischen Code gespeichert ist. Der Punkt ist nun, dass diese Proteine sich in eine dreidimensionale Struktur falten müssen (siehe Bild), um ihre biologische Funktion erfüllen zu können. Geht bei dieser Faltung etwas schief, so können Krankheiten wie Alzheimer entstehen. Darum sind Biologen sehr daran interessiert, den Mechanismus der Proteinfaltung genau zu verstehen. Doch das ist gar nicht so einfach.

SOLL EIN Computerprogramm einfach alle möglichen «Knäuel» auflisten und analysieren, in die sich ein Protein falten kann, so wird das Programm, weil die Proteine Hunderte von Aminosäuren haben können und weil es so ungeheuer viele Anordnungsvarianten gibt, auch in Milliarden von Jahren nicht zu einem Ende kommen. Und da das Problem ein NP-Problem ist, ist eine schnelle, effiziente Lösung schon deswegen unwahrscheinlich, weil dann augenblicklich Hunderte von NP-Problemen, an denen sich Heerscharen von Mathematikern die Zähne ausgebissen haben, schnell lösbar wären. Hier ist ein anderes, berühmtes NP-Problem: Ein Handlungsreisender soll 20 Städte besuchen und fragt sich, welches wohl die kürzeste Route ist, die ihn in jede Stadt genau einmal führt. Wie viele mögliche Routen gibt es? Und wie lange müsste ein Computer arbeiten, der pro Sekunde 1 Milliarde Routen durchrechnen kann?

Lösung der Kolumne vom 9. März: Die beiden Wahrscheinlichkeiten sind 66,5 Prozent und 63,7 Prozent. Man sollte also auf mindestens eine Sechs bei sechsmaligem Werfen eines Würfels wetten.