

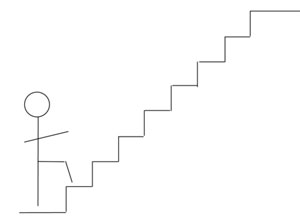
Kinder verüben alltägliche Tätigkeiten, die Erwachsene beiläufig hinter sich bringen, oftmals auf spielerische Weise. Das Ersteigen von Treppen bot für mich im Kindesalter eine beständige Versuchung zur spielerischen Ausschmückung dar. Ich konnte Treppen nicht normal hochsteigen. Ich bemühte mich entweder, so viele Stufen wie nur möglich aufs Mal zu nehmen, oder ich beschloss, erst eine Stufe, dann zwei Stufen, dann drei und so weiter zu nehmen, auch wenn es zu schmerzhaften Verrenkungen führte. Meistens ging es aber darum, Ein- und Zweistufenschritte zu variieren. Und das ist mathematisch betrachtet ungeheuer interessant, obwohl ich davon damals nicht die leiseste Ahnung hatte. Stellen wir uns also vor, da wäre eine Treppe, die immer wieder zu besteigen ist, die Treppe im eigenen Haus zum Beispiel. Wir beschliessen, immer entweder eine Stufe oder aber zwei Stufen aufs Mal zu nehmen. Und wir sehen eine besondere Herausforderung darin, diese Treppe nie zweimal auf dieselbe Art zu besteigen. Nehmen wir weiter an, die Treppe habe acht Stufen, so wie die Treppe in der Abbildung. Dann bedeuten diese Spielregeln, dass wir die Treppe heute zum Beispiel in lauter Einstufenschritten hochsteigen, morgen aber mindestens einen Zweistufenschritt einbauen und übermorgen auch wieder einen oder mehrere Zweistufenschritte einbauen müssen, aber so, dass ein Unterschied zur morgigen Variante besteht, und so weiter. Wie viele verschiedene Arten gibt es, unsere Treppe hochzusteigen?
Das ist eine wirklich spannende Frage, und sie führt zu einem wichtigen mathematischen Konzept, das zahlreiche Querbezüge zu aussermathematischen Bereichen hat. Machen wir uns also an die Beantwortung. Wir führen die Bezeichnung T(n) ein für die Anzahl Möglichkeiten, eine Treppe mit n Stufen auf die beschriebene Weise hochzusteigen. Klar ist, dass T(1)=1 ist, denn wenn eine Treppe bloss eine einzige Stufe hat, dann können wir sie bloss auf eine einzige Weise hochsteigen, indem wir nämlich einen Einstufenschritt nehmen. Klar ist ebenso, dass T(2)=2 ist, denn bei zwei Stufen können wir entweder zwei Einstufenschritte oder aber einen Zweistufenschritt nehmen. Ist dann T(3)=3? Das wäre ja immerhin naheliegend, und es ist tatsächlich zutreffend! Wir können entweder drei Einstufenschritte oder aber einen Zweistufenschritt gefolgt von einem Einstufenschritt oder aber einen Einstufenschritt gefolgt von einem Zweistufenschritt nehmen. Ist also T(4)=4? Das anzunehmen, wäre verführerisch. Aber es ist leider falsch. Es ist nämlich T(4)=5; zählen Sie ruhig nach. Die Sache ist also komplizierter, als es zunächst scheinen mag.
Hier kommt eine wunderbare rettende Idee: Am Fusse unserer 8-Stufen-Treppe haben wir genau zwei Möglichkeiten: Wir können den Aufstieg mit einem Einstufen- oder aber einem Zweistufenschritt beginnen. Falls wir mit einem Einstufenschritt beginnen, haben wir noch eine 7-Stufen-Treppe vor uns, und dafür gibt es T(7) Möglichkeiten. Wenn wir aber mit einem Zweistufenschritt beginnen, bleibt noch eine 6-Stufen-Treppe übrig, und dafür gibt es T(6) Möglichkeiten. Insgesamt ist also T(8)=T(7)+T(6) oder – allgemein – T(n)=T(n-1)+T(n-2). Das hilft enorm. Um herauszufinden, auf wie viele verschiedene Arten wir unsere 8-Stufen-Treppe ersteigen können, das heisst um T(8) zu finden, müssten wir T(7) und T(6) kennen. Um T(7) zu kennen, müssten wir T(6) und T(5) kennen. Um T(6) zu kennen, müssten wir T(5) und T(4) kennen, und so weiter. Wir müssen also zurücklaufen, um in der Lösung vorwärts zu kommen. Dieses in der Mathematik sehr häufige Konzept wird «Rekursion» genannt von dem lateinischen Verb für «zurücklaufen».
Zurücklaufen müssen wir bis zu T(1) und T(2), weil uns diese Werte ja bekannt sind. Danach können wir vorwärts rechnen: T(3)=T(2)+T(1)=2+1=3. Dann: T(4)=T(3)+T(2)=3+2=5. Dann: T(5)=T(4)+T(3)=5+3=8. Dann: T(6)=T(5)+T(4)=8+5=13. Dann: T(7)=T(6)+T(5)=13+8=21. Und endlich: T(8)=T(7)+T(6)=21+13=34. Es gibt also 34 verschiedene Arten, unsere Treppe auf die verlangte Art zu ersteigen.
Die Zahlen 1, 2, 3, 5, 8, 13, 21, 34, . . . sind überaus berühmt. Es sind die Fibonacci-Zahlen, benannt nach dem italienischen Mathematiker Leonardo Fibonacci, der sie im Jahr 1202 im Zusammenhang mit dem Anwachsen einer Kaninchenpopulation gefunden hat. Seither sind sie immer wieder aufgetaucht, in Kunst, Architektur oder der Biologie. In der Halle des Zürcher Hauptbahnhofes hat ihnen der Künstler Mario Merz eine grosse Skulptur gewidmet.
Die längste Treppe der Welt gehört übrigens dem Seilbahnunternehmen, das die Bahn von Mülenen auf den Niesen im Berner Oberland betreibt. Sie hat genau 11 674 Stufen. Es ist klar, dass T(11 674) nach der rekursiven Methode nur unendlich mühsam zu berechnen ist. Da müsste man schon eine Formel haben, die diesen Wert direkt zu berechnen gestattet, ohne zurückzurennen. Diese gibt es, und sie stammt von Binet. Und wenn Sie Interesse daran haben, dann lohnt sich eine Recherche zu diesem Thema bestimmt.