Wie viele Zahlen gibt es eigentlich? Manch einer hält das für eine banale Frage: Es gibt natürlich unendlich viele Zahlen. Zahlen entstanden ursprünglich durch den Prozess des Zählens, und wenn man Dinge zählt, kann jede der Zahlen 1, 2, 3, 4, 5, 6 . . . die Antwort sein. Eine obere Grenze gibt es offenbar nicht, denn wenn ich Buntstifte zähle und irgendeine Anzahl bekommen habe, kann ich immer noch einen weiteren Stift hinzulegen und die Anzahl damit um 1 erhöhen, egal, wie gross die Anzahl vorher gewesen ist. Zwei bekannte Mathematiker nannten das Unendliche einmal den «Wunderkrug der Mathematik»; er ist unerschöpflich, weil keine Zahl die letzte sein kann, immer ist die nächsthöhere denkbar und folglich bildbar. Also gibt es unendlich viele Zahlen.

Nun kann uns aber auffallen, dass es noch weitere, bisher unerwähnt gebliebene Zahlen gibt, negative zum Beispiel wie etwa –5 oder –2008 oder gebrochene wie 1/2 oder 7/3 oder Zahlen wie 3,141592653589793. . . (die wahnsinnig berühmt ist). Freilich brauchen uns all diese Zahlen nicht zu beschäftigen, denn wenn es schon unendlich viele natürliche Zahlen (1, 2, 3, 4, 5 . . .) gibt, bleibt die Anzahl Zahlen sicherlich unendlich, wenn wir noch einige, viele oder gar unendlich viele weitere Zahlen hinzutun.

Aber ist das nicht merkwürdig? Wenn ich 20 Buntstifte habe und noch einige weitere Stifte hinzulege, dann wird sich die Anzahl Stifte zweifellos ändern. Warum ist das bei unendlich vielen Zahlen anders? Wenn ich bereits unendlich viele natürliche Zahlen habe und nun noch alle ihre negativen Partner (also noch einmal unendlich viele Zahlen) hinzulege, warum ändert sich dann die Anzahl nicht? Oder: Wenn ich aus dem Haufen der 20 Buntstifte jeden zweiten entferne, dann halbiert sich die Anzahl; wenn ich aber aus der Menge der natürlichen Zahlen jede zweite, also zum Beispiel jede gerade Zahl, entferne, dann bleiben noch immer unendlich viele Zahlen übrig, nämlich alle ungeraden. Warum sind das nun nicht weniger Zahlen als vorher? Wir stören uns daran, dass die Phänomene im Unendlichen nicht dieselben sind wie im Endlichen, ohne allerdings auch nur die geringste Erfahrung zu haben im Umgang mit dem Unendlichen. Denn das Leben des Menschen ist auf Endlichkeit ausgelegt. Was veranlasst uns also dazu, erstaunt zu sein, wenn unendlich grosse Gesamtheiten sich anders verhalten, als wir es uns von endlichen gewohnt sind? Einer, der sich intensiv mit dem Unendlichen auseinandersetzte, war der Mathematiker Georg Cantor (1845–1918). Seine Arbeiten waren aber derart revolutionär, dass sie von vielen Zeitgenossen strikte abgelehnt oder gar bekämpft wurden. Heute gilt seine Mathematik des Unendlichen aber als eine besonders originelle, funkelnde Meisterleistung.

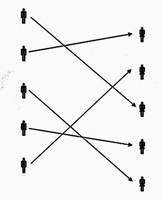
Cantor ging davon aus, dass alle Probleme verschwinden, wenn wir Mengen (seien sie nun endlich oder unendlich gross) vergleichen, anstatt sie zu zählen. Wenn wir zum Beispiel je einer Menge von Männern und einer Menge von Frauen begegnen (vgl. Abb.), so können wir, um zu entscheiden, ob sie gleich gross sind oder nicht, jeden Mann je genau einer Frau (und umgekehrt) zuordnen. Kriterien spielen bei dieser Zuordnung nicht die geringste Rolle, entscheidend ist einzig, ob diese Zuordnung «aufgeht» oder nicht. Wenn es aufgeht, dann sagen wir, die beiden Mengen seien gleich gross oder haben gleich viele Elemente. Wenn es aber nicht aufgeht, dann hat offenbar die eine Menge mehr Elemente als die andere. (In unserer Abbildung zeigt die Zuordnung, dass beide Mengen gleich gross sind.) Dieses Konzept lässt sich elegant auf die Unendlichkeit übertragen. Nehmen wir an, wir wollen die Menge aller natürlichen Zahlen (1, 2, 3, 4, 5 . . .), die vielleicht die Männer darstellen, mit der Menge aller ungeraden Zahlen (1, 3, 5, 7, 9 . . .), die dann die Frauen darstellen, miteinander vergleichen. Wir ordnen einfach dem Mann 1 die Frau 1, dem Mann 2 die Frau 3, dem Mann 3 die Frau 5, dem Mann 4 die Frau 7 usw. zu, also immer jedem Mann diejenige Frau, die dem Doppelten und dann um 1 verminderten Wert seiner eigenen Nummer entspricht. Das mag vielleicht eine entsetzliche Vorstellung für Partnervermittlungsinstitute sein, für Mathematiker ist es ganz harmlos. Entscheidend ist einzig, dass es aufgeht, dass «am Ende» weder eine Frau noch ein Mann übrig sein wird. Mit Cantor können wir nun den Schluss ziehen, dass die Menge der natürlichen Zahlen und die Menge der ungeraden Zahlen gleich gross sind. Durch Entfernen der unendlich vielen geraden Zahlen aus den natürlichen Zahlen erhält man also nicht weniger Zahlen; und das ist eine Sache, an die der Mensch sich mangels Erfahrung mit dem Unendlichen erst gewöhnen muss. Was Cantor dann aber entdeckte, erschütterte ihn über alle Massen: Er versuchte, die Menge der natürlichen Zahlen zu vergleichen mit der Menge aller Zahlen schlechthin (inklusive aller negativen und gebrochenen und anderer oben erwähnten Zahlen). Und er konnte nachweisen, dass keine solche Zuordnung möglich ist. Folglich gibt es wirklich mehr Zahlen als natürliche Zahlen, und Cantor sah sich genötigt, verschieden hohe Unendlichkeiten einzuführen. Das Unendliche ist also nicht bloss eine breiige Vorstellung von etwas Unermesslichem, es lässt sich vielmehr durch genau definierte Abstufungen erfassen...