

Als ab 1969 zwischen den USA und der damaligen UdSSR die Salt-Verhandlungen über Rüstungskontrolle (Strategic Arms Limitation Talks) stattfanden, tauchte auch die Frage auf, wie eigentlich kontrolliert werden konnte, ob die Beschränkung des Wettrüstens beiderseits eingehalten werden würde oder nicht. Insbesondere musste sichergestellt werden, dass jede Partei davon Wind bekäme, wenn die andere Partei einen unterirdischen Atombombentest durchführen würde. Die unterirdische Zündung einer Atombombe würde eine Explosion verursachen, deren Wellen in der Erdkruste gemessen werden könnten. Aber wie konnte man die von einer Bombe ausgehenden Wellen unterscheiden von den Wellen, die beispielsweise von einem natürlichen Erdbeben verursacht werden? Wellen und Schwingungen sind Phänomene, die in der Welt überaus häufig sind; die von Explosionen und Erdbeben ausgelösten Wellen sind nur zwei Beispiele unter zahllosen. Wasserwellen, das beruhigende Hin und Her des Pendels in Grossmutters Standuhr und die schwingende Saite einer Violine sind weitere Beispiele, die uns fast ständig vor Augen sind.
Etwas weniger bewusst sind wir uns wohl der Tatsache, dass wir ohne Wellen und Schwingungen weder hören noch sehen könnten. Jeder Ton, den wir hören, dringt als Schallwelle an unser Ohr und regt das Trommelfell zum Mitschwingen an, und wenn wir sehen, dechiffriert unser Auge einen Ausschnitt aus dem Spektrum elektromagnetischer Wellen, die uns überall umgeben, und unser Gehirn stellt daraus Bilder her.
Sobald man mit Schwingungen rechnerisch umgehen will – und darauf basieren Fernsehgeräte, Telefone und viele weitere Geräte –, benötigt man etwas, was über die bloss phänomenologische Beschreibung von Wellen hinausgeht: eine Formalisierung, eine mathematische Beschreibung, eine Modellbildung durch Formeln und Gleichungen, die das reale Verhalten von Wellen so präzise wie möglich einfangen. So etwas stellt die Mathematik schon lange bereit; es ist der Sinus.
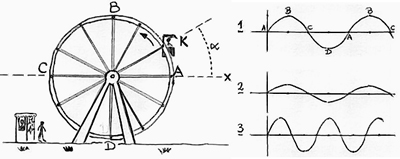
Um den Sinus zu verstehen, müssen wir uns auf den Jahrmarkt begeben, wenigstens gedanklich, und dort das Riesenrad besteigen. Stellen Sie sich also vor, Sie sitzen in der Kabine K, starten am tiefsten Punkt und werden nun langsam und im Gegenuhrzeigersinn in luftige Höhen getragen. Aus irgendeiner verrückten Laune heraus (wie sie unter Mathematikern nicht unüblich ist) beschliessen Sie, sobald Sie die Stelle A erreicht haben, die (vertikale) Distanz Ihrer Kabine zu der mit x bezeichneten Achse zu schätzen. Sie protokollieren diese Schätzungen zum Beispiel alle fünf Sekunden. Klar, im Punkt A selber ist die Distanz zur x-Achse null; das Protokoll beginnt also mit einer Null. Danach aber wächst die Distanz, anfangs ziemlich schnell, und später etwas langsamer, wenn Sie sich dem höchsten Punkt B nähern, weil Sie dort pro Zeiteinheit weniger stark an Höhe gewinnen als in der Nähe des Punktes A. In B ist die Distanz zur Achse am höchsten, nämlich gleich dem Radius des Riesenrades. Auf dem Weg von B nach C nimmt die Distanz zur Achse wieder ab, anfangs eher langsam, wenn Sie B verlassen, dann aber schneller, wenn Sie sich C nähern, und im Punkt C selber ist die Distanz zur Achse gleich null.
Auf dem Weg von C nach D befindet sich die Kabine unterhalb der Achse, weshalb Sie beschliessen, die Distanz zur Achse negativ zu zählen. Die Distanz sinkt nun also ins Negative bis zum tiefsten Wert im Punkt D, dem negativen Radius des Riesenrades. Schliesslich, zwischen D und A, wachsen die Werte wieder an bis zum Wert Null im Punkt A. Hier muss man vorsichtig sein! Zwischen D und A wachsen die Distanzwerte an, weil sie sich von tiefen negativen Zahlen zu weniger tiefen negativen Zahlen verändern. Trotzdem schrumpft der Höhenunterschied zwischen Kabine und Achse.
Nach der ersten vollen Drehung des Rades beenden Sie Ihr Protokoll, weil mit jeder weiteren Drehung die gleichen Werte sich wiederholen werden. Und dann, nach der Fahrt, besuchen Sie ein Restaurant und stellen auf Papier alle Ihre Zahlen grafisch dar. Dabei erhalten Sie eine Kurve wie die mit 1 bezeichnete Kurve in der Abbildung. Auf der waagrechten Achse stellen wir uns das Anwachsen der Zeit vor, und auf der senkrechten Achse stellen wir die Schätzwerte der Distanzen dar. Dabei entspricht die Höhe des höchsten Punktes der Kurve natürlich dem Radius und die Tiefe des tiefsten Punktes dem negativen Radius des Riesenrades. Das ist schon alles. Das ist die Sinus-Kurve.
Dank der Sinus-Kurve hat die Mathematik ein Werkzeug in der Hand, das immer dann zum Einsatz kommt, wenn Berechnungen im Zusammenhang mit einer Schwingung angestellt werden sollten, einerlei, ob die Schwingung von einer Saite, einem Erdbeben oder einem Wechselstromgenerator herrührt. Diese hohe Flexibilität verdankt Sinus der Tatsache, dass die Kurve sich jeder denkbaren Schwingung leicht anpassen kann. Denken wir nur daran, dass das Riesenrad ja auch einen kleineren Radius haben oder dass es sich schneller drehen könnte; im ersten Fall erhalten wir eher eine Kurve wie in 2 und im zweiten Fall eher eine Kurve wie in 3 dargestellt. Wie so viele andere mathematische Konzepte auch wurde das Konzept des Sinus aus cleveren Gehirnen geboren, ausgebrütet in der Absicht, etwas beizusteuern, was den Alltag des Menschen angenehmer, interessanter oder beherrschbarer macht.
Das eingangs erwähnte Problem konnte übrigens ganz einfach gelöst werden. Es gibt auf der Welt zwei Arten von Wellen: Transversalwellen, bei denen das Schwingen quer (transversal) zur Ausbreitungsrichtung geschieht, so wie bei Wasserwellen oder flatternden Flaggen, und Longitudinalwellen, bei denen das Schwingen entlang der Ausbreitungsrichtung geschieht so wie bei dem kurzen Zusammenprallen zweier Waggons, das sich dann durch alle Waggons des Zuges longitudinal ausbreitet. Eine Explosion sendet reine Longitudinalwellen aus, ein Erdbeben dagegen beide Arten von Wellen. Dieser Unterschied ist messbar, und daher könnte die unterirdische Zündung einer Atombombe jederzeit entdeckt werden.