

Beweis, dass Ruprecht ihn zerbrach!Stellen Sie sich die nicht ganz unrealistische Situation vor, dass Ihre Tochter nach Hause kommt und zu Ihnen sagt: „Du, mein Lehrer will, dass ich beweise, dass die Winkelsumme im ebenen Dreieck 180° beträgt. Kannst Du das?“ Hier ist eine Liste von (teils nicht ganz ernst gemeinten) Antworten, die Sie geben könnten:
Das Problem ist, dass das Wort ‚beweisen’ nicht nur in der Mathematik, sondern auch im Alltag verwendet wird, und es somit bei jedem von uns auf Vorstellungen und Wertungen trifft, die es in einem ganz besonderen, individuellen Licht erscheinen lassen. In der Mathematik aber wird das Wort auf eine sehr normierte, technische Weise verstanden, über die unter den Mathematikerinnen und Mathematikern weltweit Einigung besteht. Wenn es nicht gelingt, die technische Version losgelöst von der alltäglichen zu lernen, werden die ungenauen, alltäglichen Vorstellungen den Begriff ‚Beweis’ immer vernebeln und verfälschen.
Diesem klärenden Prozess hinderlich sind die zahlreichen Auftritte des Wortes ‚Beweis’ ausserhalb der Mathematik: Wenn Walter in KLEISTS „Der zerbrochene Krug“ ausruft: „Zur Sache hier. Vom Krug ist hier die Rede. – Beweis, Beweis, dass Ruprecht ihn zerbrach!“ dann werden Argumente verlangt, die das juristische System in die Lage versetzen, eine rechtskräftige Verurteilung gegen Ruprecht auszusprechen. Der Beweis besteht dann darin, das Motiv und die Gelegenheit nachzuweisen und eine möglichst lückenlose Indizienkette zu konstruieren.
Von CHURCHILL erzählt man, dass er bei einem schwachen Argument in seiner Rede, das einer kritischen Überprüfung nicht standgehalten hätte, an den Rand die Notiz „speak loud, argument weak“ kritzelte, um sich beim Reden daran zu erinnern, dass das „beweisende Argument“ überzeugender wirkt, wenn es laut und autoritär vorgebracht wird. Glücklicherweise verfehlt diese Methode ihre Wirkung in der Mathematik gänzlich. Sie können 3+4=9 noch so laut schreien, wahrer wird es dadurch nicht.
Die Beweisführungen im Gericht und auch alle nur denkbaren Tricks, mit denen man im Alltag die Überzeugungskraft eines Argumentes zu erhöhen sucht, sind nicht das, was man in der Mathematik meint, wenn man einen Beweis verlangt. Und natürlich taugen auch alle obigen Antworten nicht als Beweis, nicht einmal das Ausmessen eines Dreiecks: Messfehler wären unvermeidlich, und ausserdem könnte man zufällig ein Dreieck mit Winkelsumme 180° erwischt haben. Was die Mathematik anstrebt, ist eine Beweisführung, bei der das Behauptete immer auf etwas schon früher Bewiesenes zurückgeführt wird. Ihre Tochter könnte beispielsweise eine Parallele zu einer Dreiecksseite durch die gegenüberliegende Ecke zeichnen und die (früher bewiesene) Tatsache benutzen, dass die gleich bezeichneten Winkel gleich gross sind. Dass deren Summe 180° ist, ist dann offensichtlich, weil an der Ecke C die drei Winkel zusammen einen gestreckten Winkel ergäben.
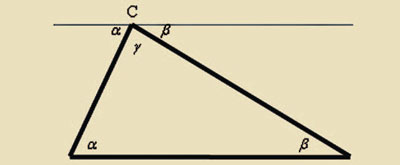
In bester mathematischer Tradition dürften Sie sich damit noch nicht zufrieden geben: Warum sind denn die gleich bezeichneten Winkel gleich gross? Warum hat ein gestreckter Winkel 180°? Und kann man durch C immer genau eine Parallele zur gegenüberliegenden Dreiecksseite ziehen? Zu ihrem Beweis muss Ihre Tochter also früher Bewiesenes heranziehen. Aber natürlich muss auch das früher Bewiesene noch früher bewiesen worden sein.
Alles Neue mit früher Bewiesenem zu begründen ist etwa so, als würde man die Existenz eines Menschen begründen, indem man seine direkten Vorfahren auflistet – und die Existenz dieser Vorfahren, indem man deren direkte Vorfahren auflistet, und die Existenz jener Vorfahren, indem man alle deren Vorfahren auflistet, usw. Dieses „Spiel“ muss ein Ende haben, denn es kann nicht unendlich viele Vorfahren geben. Und genauso muss das Beweisen in der Mathematik ein Ende finden. Es muss erste, unbeweisbare, plausible Aussagen geben. Auf diesen baut die Mathematik schrittweise auf. Und darum ist sie so sicher. Aber nur so sicher wie diese ersten, unbeweisbaren Prinzipien...