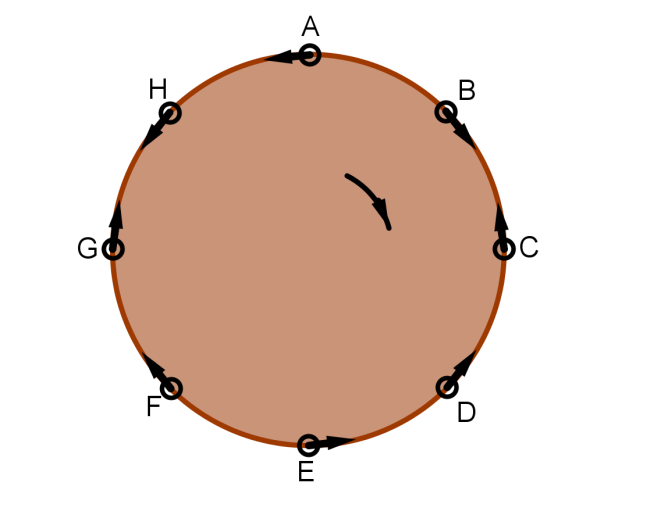
In Mathland gibt es einen Jahrmarkt, und dort ist zur Freude aller Kinder und einiger Erwachsener soeben eine neue Bahn eröffnet worden. Eine riesige kreisförmige Scheibe, deren Neigung zum Boden sich im Laufe der Fahrt verändert, dreht sich im Uhrzeigersinn, zuerst immer schneller und gegen Ende der Fahrt wieder langsamer. Am Rand der Scheibe sind Gondeln montiert, von denen jede eine Person zu fassen vermag. Zu Beginn der schwindligen Fahrt sind die Gondeln so eingestellt, dass einige Personen in Fahrtrichtung schauen, wie etwa B, F und G in der Abbildung, während alle restlichen entgegen der Fahrtrichtung blicken. Aber alle paar Sekunden drehen sich sämtliche Gondeln gleichzeitig um 180°. Wer also vor einer solchen Drehung in Fahrtrichtung geschaut hat, schaut nachher entgegen der Fahrtrichtung und umgekehrt.

Je nach Einstellung der Gondeln zu Beginn der Fahrt kann es vorkommen, dass sich zwei benachbarte Personen direkt anschauen; das ist etwa bei B und C, aber auch bei G und H der Fall, und wir wollen Nachbarn dieser Art ein Paar nennen. Andere benachbart sitzende Personen drehen sich vielleicht den Rücken zu wie etwa A und B oder auch E und F. Und solche Nachbarn nennen wir ein Anti-Paar. Klar ist auch sofort, dass sich mit einer Drehung der Gondeln jedes Paar in ein Anti-Paar und gleichzeitig jedes Anti-Paar in ein Paar verwandelt.

Leserinnen und Leser dieses Textes haben es sicher sofort bemerkt: Eine solche Bahn gibt es auf Jahrmärkten nicht; jedenfalls habe ich noch nie eine gesehen. Aus mathematischer Sicht lassen sich damit aber interessante Fragen ableiten: Wie ändert sich die Anzahl Paare mit einer Drehung der Gondeln? Wie die Anzahl Anti-Paare? Und welche Beziehung gibt es zwischen der Anzahl Paare und der Anzahl Anti-Paare? Dabei muss aber betont werden, dass wir eine Aussage machen wollen, die immer zutrifft, unabhängig davon, wie die Gondeln zu Beginn der Fahrt eingestellt sind. Wir stellen uns am besten vor, dass vor der Fahrt ein Techniker kommt und jede einzelne Gondel nach dem Zufallsprinzip – etwa aufgrund eines Münzwurfs – entweder in Fahrtrichtung oder entgegen der Fahrtrichtung einstellt. Was kann man dann über die Anzahl Paare und Antipaare aussagen?

Nun ja, klar ist, dass es nach einer Drehung aller Gondeln so viele Antipaare gibt, wie es vorher Paare gegeben hat, weil ja durch die Drehung jedes Paar in ein Anti-Paar übergeht und keine andere Konstellation in ein Anti-Paar übergehen kann. Und auch, dass es nachher so viele Paare gibt, wie es vorher Antipaare gegeben hat. Aber welche Beziehung besteht denn zwischen der Anzahl Paare und der Anzahl Anti-Paare? Im abgebildeten Beispiel sind diese Anzahlen ja gleich. Ist das ein Zufall? Könnte das auch anders sein?

Armin P. Barth ist Gymnasiallehrer an der Kantonsschule Baden und Autor. Die Lösung erscheint am nächsten Dienstag auf der Seite Leben&Wissen.